-ff-net-forum
+--Forum: Denkaufgaben
+---Topic: Wieviele Quadrate? started by ff
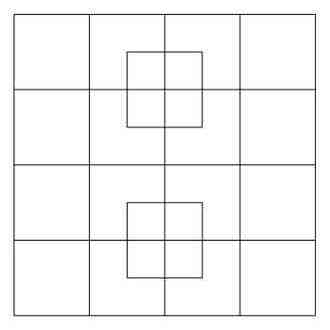
Posted by: ff on 31 Mai 2013, 11:18
Posted by: jptraun on 02 Juni 2013, 14:47
Hallo! Ich würde sagen, dass es 25 Quadrate sind. Wenn ich falsch liege, bitte den Thread löschen, damit ich mich nicht blamiere.
lg
2 Stunden später: Nach etwas Überlegung komme ich auf 31 Quadrate.
4 Stunden später (es lässt mir keine Ruh): 75 Quadrate.
Posted by: ff on 02 Juni 2013, 15:06
Daran, dass du dir nicht sicher bist, zeigt, dass die Aufgabe gar nicht so leicht ist, wie sie zunächst erscheint. Also gehts hier überhaupt nicht um's Blamieren. Warten wir einmal auf eine Bestätigung von anderen bzw. ev. auf einen Alternativ-Vorschlag. :-)
Posted by: IU on 02 Juni 2013, 16:13
Hallo
möchte mich auch beteiligen und komme auf 42 Quadrate mit großer Unsicherheit,
lg
IU
Posted by: ff on 02 Juni 2013, 16:14
Auch das ist ein interessanter Ansatz! :-)
Bis jetzt ist aber das richtige Ergebnis leider noch nicht dabei.
Posted by: Phillip on 07 Juni 2013, 11:39
Hi,
Ich würde auf 36 Quadrate kommen bin wirklich gespannt was das richtige Ergebnis ist .
LG Phillip
Posted by: ff on 07 Juni 2013, 12:50
Ich würde nocheinmal nachzählen ... ;-)
Posted by: IU on 07 Juni 2013, 18:54
Habe wieder gezählt, komme jetzt auf 65
lg
IU
Posted by: ff on 07 Juni 2013, 23:34
Mit oder ohne "Stamperl"?
Posted by: Walter on 08 Juni 2013, 22:16
35
Posted by: ff on 09 Juni 2013, 01:09
Leider nein. Jetzt wird's aber bald Zeit, dass jemand die richtige Lösung findet.
Da gibt's auch keine versteckten Tricks bei diesem Beispiel.
Es geht wirklich um das Abzählen der möglichen Quadrate.
Posted by: Trude on 09 Juni 2013, 09:29
40
Posted by: ff on 09 Juni 2013, 11:42
Bravo, genau so viele sind es! Um die Lösung gut zu veranschaulichen, musste ich teilweise "schlampig" nachzeichen ...

Posted by: Trude on 09 Juni 2013, 11:51
Wer sich bei FFs Zeichnung nicht auskennt, ich versuche es mit Worten:
1 großes 4x4
16 normale 1x1
2 normale 1x1 - in denen sich die 4 kleinen befinden
8 kleine 1/2 x 1/2
9 doppelte 2x2 3 reihen zu 3
4 dreifache 3x3 von jeder ecke ausgehend
das sind dann 40!!!!
Posted by: Phillip on 10 Juni 2013, 08:08
Ja genau diese 4 haben mir gefehlt 3x3 von jeder ecke ... #### .. war knapp dran hehe
end